Computational Chemistry and Physics on the Nanoscale
CCPN 2009
Navigation
General InformationCalculation of structure and properties using density-functional based methods
Thomas Heine
Calculations using density functional theory (DFT) are today a standard tool in theoretical chemistry and physics. It allows the efficient calculation of structures of solids, molecules, surfaces, clusters etc., with a method which is based on first principles and does not include empirical parameters. The quantum mechanical formulation of DFT allows the calculation of any property which can either be assessed through the expectation value of the Hamiltonian, or by analysis of computed static or dynamical data (Hessian, molecular dynamics trajectories etc.). In the first part of the course I will introduce the concepts of DFT and approximations which make the theory even more efficient and suitable to study systems on the nanoscale. Then, I will discuss methods to calculate spectroscopic data of nanostructures, such as NMR or IR. Emphasis will be given on the validity of common approximations.
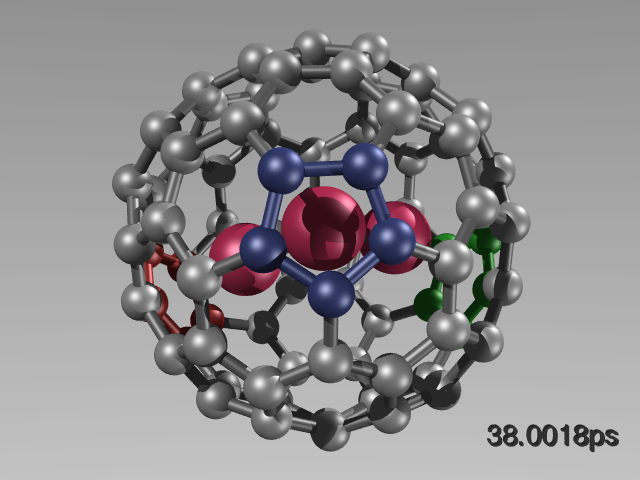
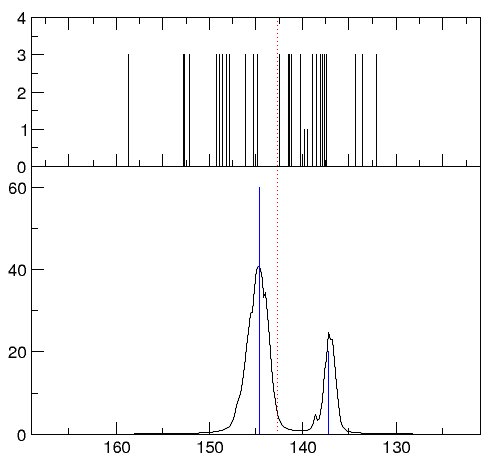
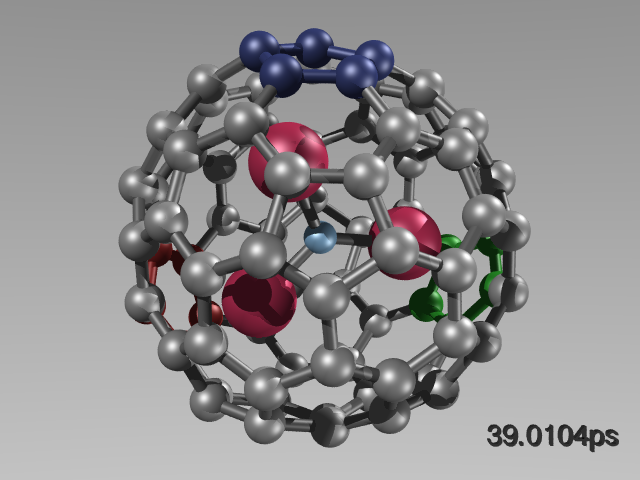
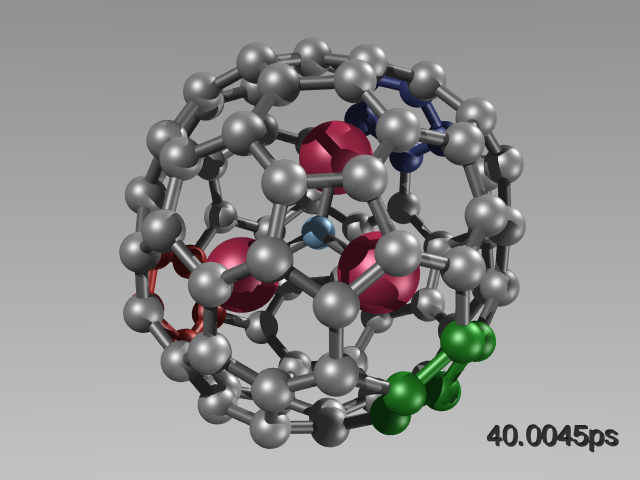
An example is given below: Sc3N@C80 is a nanostructure with promising chemical and electronic properties. The structure identification is not straight-forward: While the empty fullerene has only 2 distinct carbons, the encapsulated cluster lowers its symmetry. Standard approximations, such as geometry optimisation with subsequent property calculation fails. A DFT-based molecular dynamics simulation accompanied by many NMR computations along the trajectory reflects the experimental spectrum correctly.
|
|
|
|
|
Experimental (right, bottom, blue lines) and simulated static (right, top) and dynamic (right, bottom, solid lines) 13C NMR spectrum of Sc3N@C80 (left). The encapsulated molecule rotates and tumbles in the cage, leading to a coalescence of the 13C NMR signals to 2 distinct peaks.