Computational Chemistry and Physics on the Nanoscale
CCPN 2009
Navigation
General InformationProperties of semiconductor and metal clusters studied with global geometry-optimisation approaches
Jan-Ole Joswig
Clusters are intermediates between atoms and the solid state. Usually, they have diameters of a few Ångström up to several nanometers and contain, therefore, up to several thousand atoms. In this size range, the properties of the system of interest are affected by quantum-size effects. Thus, clusters have different properties compared to those observed in the macroscopic world. These vary, moreover, with the cluster size.
Studying the size-dependent properties of these large, but finite systems faces the problem that the number of local minima of a cluster containing N atoms is growing faster than exponentially. Thus, it is very difficult to find the global minimum structure.
The topics of the course will cover an introduction to cluster physics including experimental cluster production, examples of clusters (metal, semiconductor, and molecular clusters), the concepts magic numbers, and different methodological approaches to study clusters and their properties theoretically. Several computational methods for global geometry optimisation will be introduced and explained, e.g. genetic, grid-search, or basin-hopping algorithms. It will also be emphasized that there are many cases where a global geometry optimisation should be replaced by an “intelligent guess” of the initial structure, e.g. as part of the bulk structure of the material.
In the tutorials the students will have the opportunity to perform small simulations, e.g. a genetic-algorithms search and a simple electronic-structure calculation of small systems. Moreover, it will be taught how the obtained results, which are usually large amounts of numerical data, can be analysed and graphically depicted in a meaningful way, especially with respect to size-dependent properties.
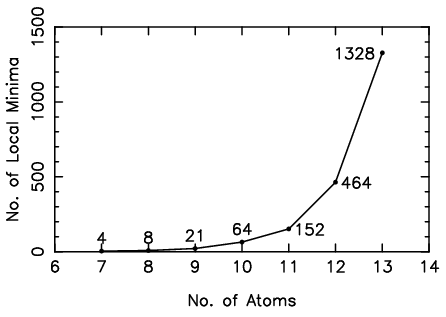
No. of local minima as function of cluster size for a Lennard-Jones pair potential