For a classical non-condensing real gas in external potential, the number density of the gas
is given by a virial expansion[35]:
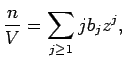 |
|
|
(1.5) |
where  is the number of particles,
is the number of particles, 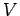 is the volume of the system, and
is the volume of the system, and
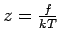 is the activity of the gas, where
is the activity of the gas, where 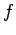 is the gas fugacity.
The first two cluster integrals
is the gas fugacity.
The first two cluster integrals 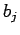 in the expansion 1.5 are given by[35]:
in the expansion 1.5 are given by[35]:
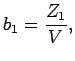 |
|
|
(1.6) |
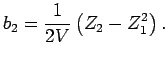 |
|
|
(1.7) |
Assuming that the adsorption potential 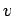 is additive with the
is additive with the 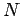 -particle contribution to the interaction energy
-particle contribution to the interaction energy 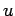 , the
, the 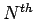 configuration integral Z
configuration integral Z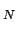 is given by[35]:
is given by[35]:
![$\displaystyle \jot9pt
Z_{N}=\mathop{\int}_{\mathbf{V}} exp\left\{-\frac{1}{kT}\...
...r_{i}\right)
+u_{N}\left(r_{1}...r_{N}\right)\right]\right\}\,dr_{1}...dr_{N} .$](img68.png) |
|
|
(1.8) |
Substituting Eq. 1.8 into 1.7, results to:
If the adsorbing potential 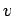 is slowly varying compared to the two-particle interaction energy
is slowly varying compared to the two-particle interaction energy 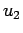 (
(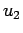 decays to zero at large distances) and
decays to zero at large distances) and 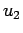 is isotropic, the integral
1.9 can be replaced by:
is isotropic, the integral
1.9 can be replaced by:
Finally, if the adsorbing potential is slowly varying in the entire integration volume, 1.10
can be further approximated by:
Therefore, the number of particles in the simulation volume 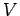 is approximately given by:
is approximately given by:
That is, for a slowly varying adsorbing potential the quantity:
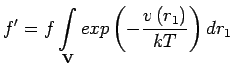 |
|
|
(1.10) |
plays the role of the fugacity.
The contributions of the intermolecular interactions within the gas itself are, to the first approximation, the same as in the free gas at the same number density.
In the case of the classical ideal gas (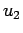 =0;
=0; 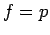 ), the integral in Eq.1.13 is the classical equilibrium constant for the ideal gas adsorption.
In order to estimate the real-gas adsorption capacity of a nanostructure, there are two quantities required:
On one hand this is the ideal gas adsorption constant K
), the integral in Eq.1.13 is the classical equilibrium constant for the ideal gas adsorption.
In order to estimate the real-gas adsorption capacity of a nanostructure, there are two quantities required:
On one hand this is the ideal gas adsorption constant K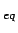 .
On the other hand the estimation of the accessible volume within the structure
.
On the other hand the estimation of the accessible volume within the structure 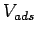 , with a slowly varying adsorption potential.
Given the external pressure
, with a slowly varying adsorption potential.
Given the external pressure 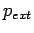 , the effective pressure of the absorbed gas inside the nanostructure
, the effective pressure of the absorbed gas inside the nanostructure  the internal pressure
the internal pressure  is
is
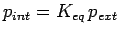 .
The experimental real gas equation of state, with the internal pressure
.
The experimental real gas equation of state, with the internal pressure 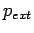 gives all further information on the guest
gives all further information on the guest host system, including the volumetric and the gravimetric storage densities.
Thus, despite the ``frozen'' host structure used in the simulation, H2 gas properties are given by the experimental equation of state[36] which covers the conditions for a conventional H2-storage applications.
host system, including the volumetric and the gravimetric storage densities.
Thus, despite the ``frozen'' host structure used in the simulation, H2 gas properties are given by the experimental equation of state[36] which covers the conditions for a conventional H2-storage applications.
Lyuben Zhechkov
2007-09-04