Methodology of calculations
The systems investigated in this work consist of different carbon modifications and hydrogen gas.
The main observable quantity is the density change of the H2 gas absorbed in the carbon materials.
Since these are complex systems, a feasible simulation requires a proper model description.
In this chapter the mathematical background of the model will to be presented along with the
relevent approximations and their advantages and disadvantages.
The results of the simulations are omitted here, but they are discussed in details in the last four chapters.
The description of the model together with its implementation is discussed in details in reference Patchkovskii2007.
The physisorbed molecular hydrogen virtually does not experience structural or electronic changes.
Therefore, the H2 guest molecule can be approximated as featureless particle with the mass of hydrogen molecule at position
guest molecule can be approximated as featureless particle with the mass of hydrogen molecule at position 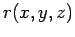 .
The arguments to treat the H2 molecule as featureless particle are discussed in details further in this chapter and are based on calculations described in Chapter 2.
This approximation allows to reduce a rather complicated model to the well known problem of a particle in three dimensional potential.
Hence, the problem to be solved is a stationary-one-particle Schrödinger equation for the motion of the mass-centre of the particle in a time-independent external potential induced by the host structure
.
The arguments to treat the H2 molecule as featureless particle are discussed in details further in this chapter and are based on calculations described in Chapter 2.
This approximation allows to reduce a rather complicated model to the well known problem of a particle in three dimensional potential.
Hence, the problem to be solved is a stationary-one-particle Schrödinger equation for the motion of the mass-centre of the particle in a time-independent external potential induced by the host structure  :
:
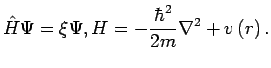 |
|
|
(1.1) |
Equation 1.1 can be discretised on a numerical grid evaluated in periodic boundary conditions, and solved using standard numerical techniques (see below).
The result is a spectrum of energies  with corresponding eigenstates
with corresponding eigenstates  , interpreted as all possible thermodynamic states of the guest molecule inside the host structure.
Since this is a one particle approximation and the guest-guest interactions are not included the so formulated problem corresponds to the ideal gas model.
The canonical one-particle partition function of the system then is given by:
, interpreted as all possible thermodynamic states of the guest molecule inside the host structure.
Since this is a one particle approximation and the guest-guest interactions are not included the so formulated problem corresponds to the ideal gas model.
The canonical one-particle partition function of the system then is given by:
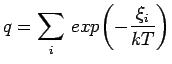 |
|
|
(1.2) |
and the corresponding density matrix is given by:
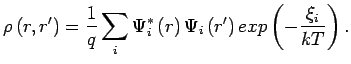 |
|
|
(1.3) |
If the same procedure is applied for a free particle then the adsorption free energy can be calculated by comparing the partition function of the gas molecule inside the host potential and the partition function of the free system (without external potential):
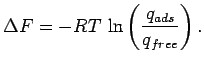 |
|
|
(1.4) |
This treatment is not only simple and straight-forward, but also of numerical advantage, as discussed below.
All other thermodynamic quantities can be calculated as derivatives of the free energy difference, using standard expressions[35].
The output quantities, such as probability densities, show the degree of delocalisation of the inserted gas molecule.
The equilibrium constant
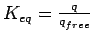 summarises the gas adsorption capabilities of the host system with respect to the free guest system as ratio between the number of adsorbed and desorbed molecules.
One special characteristic at this stage of the method is that in the ideal gas approximation the equilibrium constant
summarises the gas adsorption capabilities of the host system with respect to the free guest system as ratio between the number of adsorbed and desorbed molecules.
One special characteristic at this stage of the method is that in the ideal gas approximation the equilibrium constant 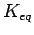 is independent on the external pressure, but depends on the temperature.
On the other hand, taking into account the quantisation of the guest translational motion, the only quantity available is the interaction free energy of a single particle in the host potential.
In real systems, however, one has to respect the interaction between the guest molecules.
Although theoretically possible, there is no straight-forward way to assess these interactions.
These interactions can be included by combining the ideal gas result and the real gas equation of state[36].
It is easy to show (see Chapter 3) that for slowly varying guest-host interaction potentials, the adsorption free energy of the classical real gas is approximately the same as the adsorption free energy of the real gas having the same density.
These assumptions are essential for the hereby presented derivation.
Therefore, detailed argumentation of the approximations inherent to this treatment is presented next.
is independent on the external pressure, but depends on the temperature.
On the other hand, taking into account the quantisation of the guest translational motion, the only quantity available is the interaction free energy of a single particle in the host potential.
In real systems, however, one has to respect the interaction between the guest molecules.
Although theoretically possible, there is no straight-forward way to assess these interactions.
These interactions can be included by combining the ideal gas result and the real gas equation of state[36].
It is easy to show (see Chapter 3) that for slowly varying guest-host interaction potentials, the adsorption free energy of the classical real gas is approximately the same as the adsorption free energy of the real gas having the same density.
These assumptions are essential for the hereby presented derivation.
Therefore, detailed argumentation of the approximations inherent to this treatment is presented next.
Subsections
Lyuben Zhechkov
2007-09-04
![]() guest molecule can be approximated as featureless particle with the mass of hydrogen molecule at position
guest molecule can be approximated as featureless particle with the mass of hydrogen molecule at position ![]() .
The arguments to treat the H2 molecule as featureless particle are discussed in details further in this chapter and are based on calculations described in Chapter 2.
This approximation allows to reduce a rather complicated model to the well known problem of a particle in three dimensional potential.
Hence, the problem to be solved is a stationary-one-particle Schrödinger equation for the motion of the mass-centre of the particle in a time-independent external potential induced by the host structure
.
The arguments to treat the H2 molecule as featureless particle are discussed in details further in this chapter and are based on calculations described in Chapter 2.
This approximation allows to reduce a rather complicated model to the well known problem of a particle in three dimensional potential.
Hence, the problem to be solved is a stationary-one-particle Schrödinger equation for the motion of the mass-centre of the particle in a time-independent external potential induced by the host structure ![]() :
: