Computational details and models
H2 molecules physisorbed on polyaromatic hydrocarbons (PAHs) have been chosen as model systems to evaluate the parameters in Eq. 1.14.
Since the dispersion interaction vanishes with a term of 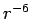 , it is expected that relatively small PAHs can depict the H2
, it is expected that relatively small PAHs can depict the H2 graphene interaction accurately enough.
The interaction energy is computed for H2 physisorbed on PAHs with different number of carbon atoms.
The smallest PAH is benzene (1 ring and 6 C
graphene interaction accurately enough.
The interaction energy is computed for H2 physisorbed on PAHs with different number of carbon atoms.
The smallest PAH is benzene (1 ring and 6 C atoms) and the largest is coronene (7 rings and 24
atoms) and the largest is coronene (7 rings and 24 C atoms) (see Fig. 2.1).
C atoms) (see Fig. 2.1).
Figure 2.1:
Topological structures of the model PAHs and ring nomenclature.
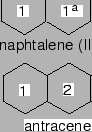 |
For the larger polyaromatic hydrocarbons Figure 2.1 also gives a nomenclature of the possible physisorption sites.
This nomenclature is used later on for evaluation of the relation between the energy interaction and the site position of the H2 molecule.
The geometrical parameters of the single PAH molecules are obtained using a low computational cost method, namely Density Functional Theory (DFT [38,44] B3LYP/6-31G* [45,46]) as implemented in Gaussian98 [47].
In order to assure the optimisation parameters, the accuracy of the DFT method has been checked for small molecules with higher level methods (Møller-Plesset perturbation theory second order[37] (MP2).
Only negligible difference ( 0.01 Å) has been found for the parameters derived with higher (MP2) and lower (DFT) levels of theory.
The DFT optimised geometry parameters of the PAHs have been used in the forthcoming calculations.
However, for the H2
0.01 Å) has been found for the parameters derived with higher (MP2) and lower (DFT) levels of theory.
The DFT optimised geometry parameters of the PAHs have been used in the forthcoming calculations.
However, for the H2 PAH complexes, a different approach has been taken.
Although, DFT performs rather well for covalent atomic structures, it is not valid for complexes where the interaction between the residues is based on dispersion forces.
In this case, ab initio methods accounting for electronic correlations are the better choice.
The H2
PAH complexes, a different approach has been taken.
Although, DFT performs rather well for covalent atomic structures, it is not valid for complexes where the interaction between the residues is based on dispersion forces.
In this case, ab initio methods accounting for electronic correlations are the better choice.
The H2 PAH distance and binding energy are therefore determined using
PAH distance and binding energy are therefore determined using post Hartree-Fock
MP2 theory2.1.
Due to incompleteness of the basis sets, an overestimation of the binding energies is expected.
Therefore basis set superposition error (BSSE) corrections are added using
the counterpoise method [49].
To estimate the performance of the different basis sets, the H2 C6H6 complex has been used.
The molecule
C6H6 complex has been used.
The molecule molecule potential energy surface has been evaluated by scanning the distance between the molecular mass centres.
Then, the basis sets have been gradually increased from 6-31G* up to aug-cc-pVQZ by reaching almost the basis set limit where the difference between the non-corrected and the BSSE corrected values is only 0.6 kJ
molecule potential energy surface has been evaluated by scanning the distance between the molecular mass centres.
Then, the basis sets have been gradually increased from 6-31G* up to aug-cc-pVQZ by reaching almost the basis set limit where the difference between the non-corrected and the BSSE corrected values is only 0.6 kJ mol
mol (see Fig. 2.2).
(see Fig. 2.2).
Figure:
Potential energy surface of H2 molecule oriented along the C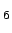 axis of the benzene molecule.
Physisorption energies (in kJ
axis of the benzene molecule.
Physisorption energies (in kJ mol
mol ) are plotted against the distance of the molecular centres (in Å). Except CCSD(T) the rest of the data is evaluated by using MP2 theory.
) are plotted against the distance of the molecular centres (in Å). Except CCSD(T) the rest of the data is evaluated by using MP2 theory.
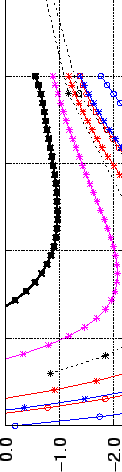 |
The corresponding bond lengths and interaction energies in the global minima of the potential wells at different levels of accuracy are given in Table 2.1.
From this table and Fig. 2.2 it can be clearly seen that in contrast to the H2 C6H6 distance, the interaction energy is extremely sensitive to the basis set at the MP2 level.
Nevertheless, by a fortuitous error cancellations the results at MP2/cc-pVTZ level give relatively good values.
They closely mimic the higher level calculations (CCSD(T) and MP2/aug-cc-pVQZ), both at the global minimum and in the asymptotic region (see Tab. 2.1 and Fig. 2.2).
Because MP2/cc-pVTZ calculations are significantly less expensive, this basis set is used for the potential energy surface (PES) characterisation in larger systems. (up to H2
C6H6 distance, the interaction energy is extremely sensitive to the basis set at the MP2 level.
Nevertheless, by a fortuitous error cancellations the results at MP2/cc-pVTZ level give relatively good values.
They closely mimic the higher level calculations (CCSD(T) and MP2/aug-cc-pVQZ), both at the global minimum and in the asymptotic region (see Tab. 2.1 and Fig. 2.2).
Because MP2/cc-pVTZ calculations are significantly less expensive, this basis set is used for the potential energy surface (PES) characterisation in larger systems. (up to H2 coronene see Fig. 2.1)
This basis set has been used as well for test calculations with coupled-cluster treatment of the electron correlation.
In the global PES minimum, H2 has been found to be aligned along the C
coronene see Fig. 2.1)
This basis set has been used as well for test calculations with coupled-cluster treatment of the electron correlation.
In the global PES minimum, H2 has been found to be aligned along the C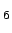 symmetry (perpendicular orientation see Fig. 2.3 Left) axis of benzene at a distance
symmetry (perpendicular orientation see Fig. 2.3 Left) axis of benzene at a distance 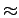 3.1 Å between the mass-centres of H2 and C6H6.
3.1 Å between the mass-centres of H2 and C6H6.
Figure:
Three high symmetry orientations of H2 on top of the benzene's centre. C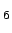
 (Left), C
(Left), C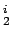
 (Middle), C
(Middle), C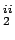
 (Right),
(Right),
|
The energy profile shows a typical London-type 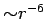 long-range behaviour (Fig. 2.2).
More sophisticated correlation treatment (CCSD(T)/cc-pVTZ) reduces the H2
long-range behaviour (Fig. 2.2).
More sophisticated correlation treatment (CCSD(T)/cc-pVTZ) reduces the H2 benzene interaction by 0.9 kJ
benzene interaction by 0.9 kJ mol
mol [50] (
[50] (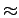 20%) comparing with MP2/cc-pVTZ values, whereas the geometry remains essentially unchanged.
Similar trends are observed for the other two high symmetry orientations (see Fig. 2.3 Middle and Right) of the hydrogen with respect to a benzene molecule.
The energy profiles of these two orientations are indistinguishable at this level of calculations and for readability only one of them is shown on Figure 2.4.
Besides the surprisingly good performance found for cc-pVTZ basis set the calculations and the counter poise procedure shows that there is no significant energetic difference between different orientations (normal and parallel).
20%) comparing with MP2/cc-pVTZ values, whereas the geometry remains essentially unchanged.
Similar trends are observed for the other two high symmetry orientations (see Fig. 2.3 Middle and Right) of the hydrogen with respect to a benzene molecule.
The energy profiles of these two orientations are indistinguishable at this level of calculations and for readability only one of them is shown on Figure 2.4.
Besides the surprisingly good performance found for cc-pVTZ basis set the calculations and the counter poise procedure shows that there is no significant energetic difference between different orientations (normal and parallel).
Figure:
Potential energy surface of H2 parallel to the benzene plane at the MP2 level. (see Fig. 2.3 Middle and Left) Comparison with the (normal) perpendicular orientation is given as well. The potential energy surfaces for the parallel orientations are identical at this level of calculation therefore only one of them is given for readability.
 |
Figure 2.4 shows the PES for two high symmetry orientations of the hydrogen molecule when its H-H axis is parallel to the plane of benzene compared with the perpendicular orientations(see Fig. 2.3).
The minima in the PESs well depth show small difference (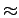 1.5 kJ
1.5 kJ mol
mol ) compared with perpendicular orientation and no difference when H2 rotates in the plane complanar to the benzene plane.
However, at higher temperatures these different orientations are expected to be indistinguishable (see section 1.1.4).
Further on, for the sake of simplicity, the conclusions are based only on the models in which H2 is perpendicularly oriented with respect to the plane of PAHs.
The distance between the mass centres of the residues in the H2-PAH complexes is found to be 3.08 Å.
A full geometry optimisation at the MP2/cc-pVTZ level for I, II, and III complexes (see Fig. 2.1) shows that the PAH size have negligible effect on the H2-PAH bond length.
Neither has the adsorption site of the PAH, as long as the hydrogen molecule is positioned on top of the ring centre.
The covalent bond lengths in the three H2-PAHs (I, II, and III) complexes change within 0.006 Å.
Whereas, the distance between H2 and PAHs in these benchmark complexes, differs by less than 0.01 Å.
The interaction energy in the ground state, estimated by the PES scan underestimate the full optimisation energy by less than 0.02 kJ
) compared with perpendicular orientation and no difference when H2 rotates in the plane complanar to the benzene plane.
However, at higher temperatures these different orientations are expected to be indistinguishable (see section 1.1.4).
Further on, for the sake of simplicity, the conclusions are based only on the models in which H2 is perpendicularly oriented with respect to the plane of PAHs.
The distance between the mass centres of the residues in the H2-PAH complexes is found to be 3.08 Å.
A full geometry optimisation at the MP2/cc-pVTZ level for I, II, and III complexes (see Fig. 2.1) shows that the PAH size have negligible effect on the H2-PAH bond length.
Neither has the adsorption site of the PAH, as long as the hydrogen molecule is positioned on top of the ring centre.
The covalent bond lengths in the three H2-PAHs (I, II, and III) complexes change within 0.006 Å.
Whereas, the distance between H2 and PAHs in these benchmark complexes, differs by less than 0.01 Å.
The interaction energy in the ground state, estimated by the PES scan underestimate the full optimisation energy by less than 0.02 kJ mol
mol .
In order to extend the grid of the potential energy surface, H2 coordinates other than those laying on the C
.
In order to extend the grid of the potential energy surface, H2 coordinates other than those laying on the C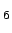 axis of benzene, have been investigated as well.
It was found that for sites as on-top-of-atoms and on-top-of-bonds hydrogen experience slightly weaker interaction than on the top of the benzene's centre (by
axis of benzene, have been investigated as well.
It was found that for sites as on-top-of-atoms and on-top-of-bonds hydrogen experience slightly weaker interaction than on the top of the benzene's centre (by 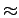 1.2 kJ
1.2 kJ mol
mol at MP2/cc-pVTZ level).
For larger systems as coronene these values have been found to be even smaller (
at MP2/cc-pVTZ level).
For larger systems as coronene these values have been found to be even smaller (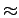 0.8 kJ
0.8 kJ mol
mol ), which indicates a softening of the potential with the increase of the sorbent surface.
These numbers are in agreement with reported results at various theoretical levels [51,52,53].
To avoid unphysical conclusions, all approximations and models employed here, except the MP2 theory, are chosen to underestimate the interaction, so that final physisorption energy should be slightly lower.
), which indicates a softening of the potential with the increase of the sorbent surface.
These numbers are in agreement with reported results at various theoretical levels [51,52,53].
To avoid unphysical conclusions, all approximations and models employed here, except the MP2 theory, are chosen to underestimate the interaction, so that final physisorption energy should be slightly lower.
Because in larger PAHs the 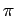 - system does not change dramatically its nature the physisorption is assumed to obey the same trends as with benzene ring.
Therefore, the larger H2-PAH complexes are build according to the following assumptions:
the strongest interaction is on top of the hexagon ring's centre and the hydrogen molecule is oriented along the C
- system does not change dramatically its nature the physisorption is assumed to obey the same trends as with benzene ring.
Therefore, the larger H2-PAH complexes are build according to the following assumptions:
the strongest interaction is on top of the hexagon ring's centre and the hydrogen molecule is oriented along the C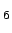 axis.
The validity of these assumptions has been proven by calculations repeathing the H2-benzene procedure for naphthalene and anthracene.
Thus, knowing the performance and the errors which can be introduced with MP2/cc-pVTZ level of calculations and the basic trends for the smaller systems of the series (see Fig. 2.1), the building of larger models is done in the following manner:
a) optimise the building blocks of the H2
axis.
The validity of these assumptions has been proven by calculations repeathing the H2-benzene procedure for naphthalene and anthracene.
Thus, knowing the performance and the errors which can be introduced with MP2/cc-pVTZ level of calculations and the basic trends for the smaller systems of the series (see Fig. 2.1), the building of larger models is done in the following manner:
a) optimise the building blocks of the H2 PAH complex by using B3LYP/6-31G* level of theory,
b) build the complexes with different number of hydrogen molecules situated at the centres of symmetrically distinguishable
benzene rings and c) calculate the energy of interaction at the equilibrium distance (3.08 Å).
PAH complex by using B3LYP/6-31G* level of theory,
b) build the complexes with different number of hydrogen molecules situated at the centres of symmetrically distinguishable
benzene rings and c) calculate the energy of interaction at the equilibrium distance (3.08 Å).
Lyuben Zhechkov
2007-09-04
![]() , it is expected that relatively small PAHs can depict the H2
, it is expected that relatively small PAHs can depict the H2![]() graphene interaction accurately enough.
The interaction energy is computed for H2 physisorbed on PAHs with different number of carbon atoms.
The smallest PAH is benzene (1 ring and 6 C
graphene interaction accurately enough.
The interaction energy is computed for H2 physisorbed on PAHs with different number of carbon atoms.
The smallest PAH is benzene (1 ring and 6 C![]() atoms) and the largest is coronene (7 rings and 24
atoms) and the largest is coronene (7 rings and 24![]() C atoms) (see Fig. 2.1).
C atoms) (see Fig. 2.1).
![]() C6H6 complex has been used.
The molecule
C6H6 complex has been used.
The molecule![]() molecule potential energy surface has been evaluated by scanning the distance between the molecular mass centres.
Then, the basis sets have been gradually increased from 6-31G* up to aug-cc-pVQZ by reaching almost the basis set limit where the difference between the non-corrected and the BSSE corrected values is only 0.6 kJ
molecule potential energy surface has been evaluated by scanning the distance between the molecular mass centres.
Then, the basis sets have been gradually increased from 6-31G* up to aug-cc-pVQZ by reaching almost the basis set limit where the difference between the non-corrected and the BSSE corrected values is only 0.6 kJ![]() mol
mol![]() (see Fig. 2.2).
(see Fig. 2.2).


![]() - system does not change dramatically its nature the physisorption is assumed to obey the same trends as with benzene ring.
Therefore, the larger H2-PAH complexes are build according to the following assumptions:
the strongest interaction is on top of the hexagon ring's centre and the hydrogen molecule is oriented along the C
- system does not change dramatically its nature the physisorption is assumed to obey the same trends as with benzene ring.
Therefore, the larger H2-PAH complexes are build according to the following assumptions:
the strongest interaction is on top of the hexagon ring's centre and the hydrogen molecule is oriented along the C![]() axis.
The validity of these assumptions has been proven by calculations repeathing the H2-benzene procedure for naphthalene and anthracene.
Thus, knowing the performance and the errors which can be introduced with MP2/cc-pVTZ level of calculations and the basic trends for the smaller systems of the series (see Fig. 2.1), the building of larger models is done in the following manner:
a) optimise the building blocks of the H2
axis.
The validity of these assumptions has been proven by calculations repeathing the H2-benzene procedure for naphthalene and anthracene.
Thus, knowing the performance and the errors which can be introduced with MP2/cc-pVTZ level of calculations and the basic trends for the smaller systems of the series (see Fig. 2.1), the building of larger models is done in the following manner:
a) optimise the building blocks of the H2![]() PAH complex by using B3LYP/6-31G* level of theory,
b) build the complexes with different number of hydrogen molecules situated at the centres of symmetrically distinguishable
benzene rings and c) calculate the energy of interaction at the equilibrium distance (3.08 Å).
PAH complex by using B3LYP/6-31G* level of theory,
b) build the complexes with different number of hydrogen molecules situated at the centres of symmetrically distinguishable
benzene rings and c) calculate the energy of interaction at the equilibrium distance (3.08 Å).