SWCNT and bundles
The series of geometries discussed hereby consists in nanotubes having diameters between 4 and 16 Å, including only zigzag and armchair types with Hamada indexes (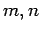 ) respectively
) respectively 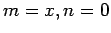 and
and 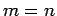 (where
(where 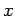 is integer).
The calculations have been carried out in periodic boundary conditions according to the methodology explained in Chapter 1.
Structures possessing
is integer).
The calculations have been carried out in periodic boundary conditions according to the methodology explained in Chapter 1.
Structures possessing 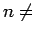 0 or
0 or 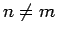 have not been considered in the calculations since this would lead to a large simulation cells.
The C
have not been considered in the calculations since this would lead to a large simulation cells.
The C C bond length has been chosen to be
C bond length has been chosen to be  =1.421 Å, as it is accepted in the literature[57] for the carbon
=1.421 Å, as it is accepted in the literature[57] for the carbon carbon distance in graphite.
In order to calculate the physisorption properties of the inner and outer tube surfaces, the primitive unit cells of the nanotubes have been repeated in two ways:
carbon distance in graphite.
In order to calculate the physisorption properties of the inner and outer tube surfaces, the primitive unit cells of the nanotubes have been repeated in two ways:
- replication only along the nanotube axes
- replication in all directions so that the nanotubes are arranged in a bundle with hexagonal symmetry and distance between the nanotubes walls of 3.41 Å coresponding to th distance between the graphene layers in graphite
In the first case the potential has been evaluated in a rectangular box with height equal to the  (along the axis of the tube) parameter of the unit cell, and sites (
(along the axis of the tube) parameter of the unit cell, and sites (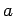 and
and 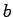 parameters) equal to the diameter of the nanotubes.
In the second case the unit cell consists of two single nanotube primitive cells, so that repeated in
parameters) equal to the diameter of the nanotubes.
In the second case the unit cell consists of two single nanotube primitive cells, so that repeated in 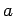 and
and 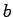 directions they create hexagonal arrangement of nanotubes (infinite bundle of nanotubes).
The distance between the nanotubes in a bundle is defined as
directions they create hexagonal arrangement of nanotubes (infinite bundle of nanotubes).
The distance between the nanotubes in a bundle is defined as 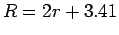 Å where
Å where 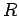 is the distance between the tube axes and
is the distance between the tube axes and 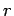 is the nanotube radius.
In both cases the potential in the box has been contributed from the 15 nearest unit cells along the tube axis, both backwards and forewards.
For the zigzag structures (
is the nanotube radius.
In both cases the potential in the box has been contributed from the 15 nearest unit cells along the tube axis, both backwards and forewards.
For the zigzag structures (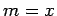
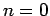 and
and 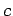 = 4.26 Å) the unit cells were chosen to correspond to the primitive cell of the nanotubes.
In order to avoid the quantum confinement effects, because of the small lattice vector in
= 4.26 Å) the unit cells were chosen to correspond to the primitive cell of the nanotubes.
In order to avoid the quantum confinement effects, because of the small lattice vector in 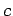 direction (
direction (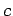 = 2.46 Å), the unit cell of the armchair modification (
= 2.46 Å), the unit cell of the armchair modification (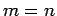 ) consists of two primitive cells repeated in the
) consists of two primitive cells repeated in the 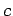 direction.
Since the atoms on the walls are not laying in one plane, especially for tubes with very small diameter, the radius is taken as a mean distance between the axis and the atoms on the tube wall.
Although, the geometrical parameters of the bundles and the nanotubes themself are close to the experimental values, it is worth to mention that they do not pretend to be very accurate.
Instead, the models are build so that they demonstrate the general trends in the hydrogen storage capacities of these structures with respect to their geometrical properties.
direction.
Since the atoms on the walls are not laying in one plane, especially for tubes with very small diameter, the radius is taken as a mean distance between the axis and the atoms on the tube wall.
Although, the geometrical parameters of the bundles and the nanotubes themself are close to the experimental values, it is worth to mention that they do not pretend to be very accurate.
Instead, the models are build so that they demonstrate the general trends in the hydrogen storage capacities of these structures with respect to their geometrical properties.
Subsections
Lyuben Zhechkov
2007-09-04