CIG storage capacities
The procedure described in Chapter 1 and demonstrated in Chapter 2 is now applied for more realistic system which has C60 as support spacers in order to keep graphene sheets away from each other.
Thus, the supercell unit consists of two fullerenes situated above a graphene sheet.
The distances between the fullerenes themself, the graphene sheet, and the parameters of the unit cell have been chosen so that they reproduce accurate enough the optimised periodic structure of CIG [83].
Since a penetration of the guest molecule trough the graphene sheet is most unlikely at moderate temperature conditions, (see Chapter 3.1) the highly repulsive potential near the graphene surfaces (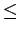 1 Å) has been excluded from the simulated volume.
This has been done in order to avoid the attractive artifacts of the
1 Å) has been excluded from the simulated volume.
This has been done in order to avoid the attractive artifacts of the 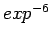 potential close to the nuclei and reduce the requirements for high-frequency basis set components.
potential close to the nuclei and reduce the requirements for high-frequency basis set components.
The evaluation of the potential in this model shows that the H2 host interaction is attractive in the space between the fullerene cages and graphene.
However, it shows an even higher attractive (-32 kJ
host interaction is attractive in the space between the fullerene cages and graphene.
However, it shows an even higher attractive (-32 kJ mol
mol ) potential in the interior of the fullerenes.
Since this volume is expected to be inaccessible for hydrogen molecules because of the high energetic threshold, the interaction potential on the
grid points inside of the cages are set up to have repulsive values.
A slice of the attractive interaction potential in the so modified H2
) potential in the interior of the fullerenes.
Since this volume is expected to be inaccessible for hydrogen molecules because of the high energetic threshold, the interaction potential on the
grid points inside of the cages are set up to have repulsive values.
A slice of the attractive interaction potential in the so modified H2 CIG model is shown on Figure 4.1.
CIG model is shown on Figure 4.1.
Figure:
The interaction potential between H2 and C60-intercalated
graphite (H2-CIG). The figure shows potential energy isosurfaces
in a diagonal cut through the unit cell.
|
To further calculate the H2-CIG storage abilities the procedure of calculating the 3D-potential and the thermodynamical functions of H2 generally follows the steps described in details in section 3.2.
Since a part of the space reachable by H2 though being attractive for the hydrogen molecule is not included in the total attractive contribution, the volume excluding that part is called ``active volume''; it describes only the realistically attractive guest host potential.
For CIG, the active volume is found in the fossae and grooves between the fullerenes and the graphene sheets, where the potential reaches values of
host potential.
For CIG, the active volume is found in the fossae and grooves between the fullerenes and the graphene sheets, where the potential reaches values of  12.5 kJ
12.5 kJ mol
mol .
On the contrary, at the points of closest (distances of about 3.5 Å comparable with the one of the graphene
.
On the contrary, at the points of closest (distances of about 3.5 Å comparable with the one of the graphene graphene distance in graphite) fullerene
graphene distance in graphite) fullerene fullerene and fullerene
fullerene and fullerene graphene distances the H2
graphene distances the H2 host potential becomes repulsive.
The active volume of CIG has been determined by numerical integration, and is found to be about 19% of the total cell volume.
In comparison, the same structure without fullerene spacers has an active volume of 62%.
This makes the active volume of CIG about three times smaller because of the excluded C60 volumes.
On the other hand, comparison of the interaction free energy of CIG and hypothetical graphite with the same interlayer
distance as function of the temperature shows interesting results (Fig. 4.2 Left).
host potential becomes repulsive.
The active volume of CIG has been determined by numerical integration, and is found to be about 19% of the total cell volume.
In comparison, the same structure without fullerene spacers has an active volume of 62%.
This makes the active volume of CIG about three times smaller because of the excluded C60 volumes.
On the other hand, comparison of the interaction free energy of CIG and hypothetical graphite with the same interlayer
distance as function of the temperature shows interesting results (Fig. 4.2 Left).
Figure:
The dependence of free energy (Left) and equilibrium constant (Right)
with respect to the temperature, within the ideal gas approximation
for H2. Values for C60 intercalated graphite (circles) are compared
with those of hypothetical graphite with the same interlayer distance
(crosses).
intercalated graphite (circles) are compared
with those of hypothetical graphite with the same interlayer distance
(crosses).
|
Over the range of 50 K to ambient temperature, the spacers double the interaction free energy of CIG with H2 compared to the structure without spacers (C60s).
However, the supporting effect for H2 storage due to lower free energy is partially compensated by the reduction of active volume, which is now taken by the fullerene cages.
The resulting relative storage capacity, compared with free H2 gas at the same temperature and pressure, is given by the corresponding equilibrium constant (Fig. 4.2 Right).
Since CIG has, in fact, higher carbon density then hypothetical graphite with same interlayer distance, the structure should be able to increase the internal pressure of the gas in order to compensate its weight in the gravimetric ratio.
In other words the resulting storage capacity, compared with free H2 gas at the same temperature and pressure, will depend on the capabilities of how many times the system can increase the abundance of the gas molecules.
Thus 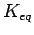 values suggest as first approximation that storage capacities might become interesting for practical applications at relatively high temperatures.
However, despite the higher CIG values for the equilibrium constant compared with the hypothetical structures in Chapter 3, the evaluated gravimetric and volumetric storage capacities look very similar. (see Figures 4.3 and 3.2)
values suggest as first approximation that storage capacities might become interesting for practical applications at relatively high temperatures.
However, despite the higher CIG values for the equilibrium constant compared with the hypothetical structures in Chapter 3, the evaluated gravimetric and volumetric storage capacities look very similar. (see Figures 4.3 and 3.2)
Figure:
Gravimetric (Left) and Volumetric (Right) storage capacities of
CIG are given for various temperatures (colour
coded). For bold lines, the approximation is within the limits (pressure and temperature) of the real gas
equation of state [36].
The targets [4] for automotive
applications (Gwt) 6.0 %,(V) 44.4 cm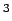 /mol) are indicated as
horizontal lines.
/mol) are indicated as
horizontal lines.
|
These results however, are somehow unexpected
since more than half of the space available in graphite (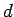 = 13 Å)
is already occupied with fullerenes. Possible explanation is the more effective overlap
of the C
= 13 Å)
is already occupied with fullerenes. Possible explanation is the more effective overlap
of the C atoms contributions coming from the fullerene cages, especially in the
regions of the grooves and fossae, and hence the increased free interaction energy in these regions.
atoms contributions coming from the fullerene cages, especially in the
regions of the grooves and fossae, and hence the increased free interaction energy in these regions.
A better understanding can be given in terms of density of states (DOS). The density of H2 states for the CIG and hypothetical graphite with the same interlayer distance are given in Figure 4.4.
Figure:
Density of states (DOS) of molecular hydrogen in C60 intercalated graphite, hypothetical graphite with same interlayer
distance and of a potential-free simulation box.
intercalated graphite, hypothetical graphite with same interlayer
distance and of a potential-free simulation box.
|
It shows two main differences between CIG and graphite system:
The C60 spacers reduce the total amount of available binding states, which is a direct consequence of the reduced total space, which may be occupied by hydrogen between the two graphene sheets (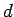 = 13 Å).
On the other hand, the spacers lower the energy levels populated by H2.
As a consequence, the internal pressure in CIG is higher and leads to hydrogen densities of about 20 % greater (at T=200 K, P=5 MPa), than in the hypothetical graphite model (see Figures 3.2 and 4.3).
Although, high densities are estimated for H2 physisorbed in CIG, the gravimetric capacity does not show such a good trend because of the high carbon density of the material.
Further tuning of the system may increase the H2/carbon mass ratio, but not out of the context of the volumetric capacity.
It is worth to mention as well, that since the potential in the grooves and fossae changes reasonably vast this may lead to big error bars in the estimated capacities.
Thus presumably lower hydrogen densities may be expected.
However, properly designed cavities in the carbon materials may lead to considerable increase in the sobbing abilities of the carbon materials.
= 13 Å).
On the other hand, the spacers lower the energy levels populated by H2.
As a consequence, the internal pressure in CIG is higher and leads to hydrogen densities of about 20 % greater (at T=200 K, P=5 MPa), than in the hypothetical graphite model (see Figures 3.2 and 4.3).
Although, high densities are estimated for H2 physisorbed in CIG, the gravimetric capacity does not show such a good trend because of the high carbon density of the material.
Further tuning of the system may increase the H2/carbon mass ratio, but not out of the context of the volumetric capacity.
It is worth to mention as well, that since the potential in the grooves and fossae changes reasonably vast this may lead to big error bars in the estimated capacities.
Thus presumably lower hydrogen densities may be expected.
However, properly designed cavities in the carbon materials may lead to considerable increase in the sobbing abilities of the carbon materials.
Lyuben Zhechkov
2007-09-04
![]() 1 Å) has been excluded from the simulated volume.
This has been done in order to avoid the attractive artifacts of the
1 Å) has been excluded from the simulated volume.
This has been done in order to avoid the attractive artifacts of the ![]() potential close to the nuclei and reduce the requirements for high-frequency basis set components.
potential close to the nuclei and reduce the requirements for high-frequency basis set components.
![]() host interaction is attractive in the space between the fullerene cages and graphene.
However, it shows an even higher attractive (-32 kJ
host interaction is attractive in the space between the fullerene cages and graphene.
However, it shows an even higher attractive (-32 kJ![]() mol
mol![]() ) potential in the interior of the fullerenes.
Since this volume is expected to be inaccessible for hydrogen molecules because of the high energetic threshold, the interaction potential on the
grid points inside of the cages are set up to have repulsive values.
A slice of the attractive interaction potential in the so modified H2
) potential in the interior of the fullerenes.
Since this volume is expected to be inaccessible for hydrogen molecules because of the high energetic threshold, the interaction potential on the
grid points inside of the cages are set up to have repulsive values.
A slice of the attractive interaction potential in the so modified H2![]() CIG model is shown on Figure 4.1.
CIG model is shown on Figure 4.1.