Mono- and double layer models
The adsorption potential of H2 on graphene surface is calculated as a two-dimensional, periodic graphene sheet with experimental C C (
C (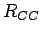 =1.421 Å) distance[57].
Contributions to the potential from 30 nearest primitive unit cells are included along the in-plane
=1.421 Å) distance[57].
Contributions to the potential from 30 nearest primitive unit cells are included along the in-plane 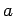 and
and 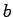 directions of a graphene sheet.
For the double-layer structures, the potential of only two layers (``above'' and ``below'' the H2) is included.
For short inter-layer separations, attraction due to the second-neighbour layer may further increase interaction energies.
Nonetheless, this effect was not considered in the simulations for reasons explaned in Chapter 1.
The resulting potential of the two-dimensionally periodic double
directions of a graphene sheet.
For the double-layer structures, the potential of only two layers (``above'' and ``below'' the H2) is included.
For short inter-layer separations, attraction due to the second-neighbour layer may further increase interaction energies.
Nonetheless, this effect was not considered in the simulations for reasons explaned in Chapter 1.
The resulting potential of the two-dimensionally periodic double layered graphene model is illustrated in Fig. 3.1.
layered graphene model is illustrated in Fig. 3.1.
Figure:
Potential energy surface for H2 adsorbed between graphene sheets separated by 8Å.
The isosurfaces correspond to potential energy of, respectively,  9.0 (deep blue),
9.0 (deep blue),  7.0 (light-blue),
7.0 (light-blue),  5.0 (green-blue),
5.0 (green-blue),
 3.0 (yellow), 0.0 (orange), and 1.0 (red) kJ
3.0 (yellow), 0.0 (orange), and 1.0 (red) kJ mol
mol .
The coordinates are given in Å. The carbon atoms of the graphene surfaces are at z = 0.0 and 8 Å, but drawn here for clarity
at z = 2 Å (bottom) and 6 Å (top).
.
The coordinates are given in Å. The carbon atoms of the graphene surfaces are at z = 0.0 and 8 Å, but drawn here for clarity
at z = 2 Å (bottom) and 6 Å (top).
|
Free energies of adsorption were calculated within the ideal gas approximation (see Eq. 1.4).
The canonical partition functions 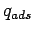 and
and 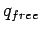 (see Eq. 1.2)
are obtained from the energy levels
(see Eq. 1.2)
are obtained from the energy levels 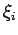 , determined by solving the stationary one-particle Schrödinger equation for H2 motion in the adsorbing potential (
, determined by solving the stationary one-particle Schrödinger equation for H2 motion in the adsorbing potential (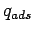 ) and in free space (
) and in free space (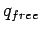 ).
The thermodynamic functions (e.g.
).
The thermodynamic functions (e.g. 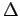 E,
E, 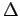 S,
S, 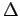 F) may be obtained using standard expressions[35,58].
The time-independent Schrödinger equation is solved for a single featureless particle with the mass of a hydrogen molecule.
These calculations employ periodic boundary conditions and a plane wave basis set.
In order to accelerate convergence of the free energies with the plane wave cutoff, identical unit cell dimensions and plane wave cutoffs are used for calculation of
F) may be obtained using standard expressions[35,58].
The time-independent Schrödinger equation is solved for a single featureless particle with the mass of a hydrogen molecule.
These calculations employ periodic boundary conditions and a plane wave basis set.
In order to accelerate convergence of the free energies with the plane wave cutoff, identical unit cell dimensions and plane wave cutoffs are used for calculation of 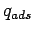 and
and 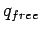 .
.
The rectangular unit cell is obtained by replicating the primitive unit cell (
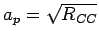 ,
, 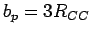 ,
, 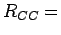 1.421 Å) in
1.421 Å) in 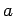 and
and 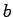 directions.
However, to avoid the attractive artifacts of the
directions.
However, to avoid the attractive artifacts of the 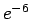 potential close to the nuclei and reduce the requirements for high-frequency basis set components, the simulation cell extent in the
potential close to the nuclei and reduce the requirements for high-frequency basis set components, the simulation cell extent in the 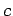 direction
direction for this particular series of structures (see section 1.1.1)
for this particular series of structures (see section 1.1.1) was truncated by
was truncated by 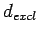 (1.0
(1.0 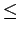
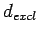
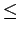 2.0 Å) in the vicinity of the graphene sheet(s).
For double-layer structures with interlayer spacing
2.0 Å) in the vicinity of the graphene sheet(s).
For double-layer structures with interlayer spacing 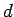 , the unit cell extent in the
, the unit cell extent in the 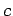 direction is, therefore,
direction is, therefore,
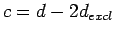 . Single-layer simulations were
performed by using the same periodic boundary conditions, but the
interlayer spacing
. Single-layer simulations were
performed by using the same periodic boundary conditions, but the
interlayer spacing 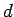 was chosen to be large. The unit cell parameters,
together with the plane wave cutoffs, are given in Table 3.1.
was chosen to be large. The unit cell parameters,
together with the plane wave cutoffs, are given in Table 3.1.
The contributions due to the adsorption-induced changes in the internal motion (rotation and vibration see Chapter 1.1.4) of the H2 molecules are neglected.
The consequences of this approximation can be understood by using the PES of the H2 benzene complex.
Because of the stiffness of the H2 molecule, only the change in the zero-point energy can contribute at temperatures of interest.
At the
benzene complex.
Because of the stiffness of the H2 molecule, only the change in the zero-point energy can contribute at temperatures of interest.
At the 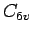 minimum of the H2
minimum of the H2 benzene PES, the calculated H2 harmonic vibrational frequency is of 4,494 cm
benzene PES, the calculated H2 harmonic vibrational frequency is of 4,494 cm , 30 cm
, 30 cm below the free H2 molecule.
Indeed, the softening of the H2 vibrational mode appears to be a general trend upon physisorption of this molecule as demonstrated elsewhere in ref. Patchkovskii2003.
However, at 200 K, the (neglected) increase in the adsorption constant is
below the free H2 molecule.
Indeed, the softening of the H2 vibrational mode appears to be a general trend upon physisorption of this molecule as demonstrated elsewhere in ref. Patchkovskii2003.
However, at 200 K, the (neglected) increase in the adsorption constant is
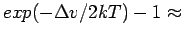 11 %, often leading to a slight underestimation of the storage capacity.
11 %, often leading to a slight underestimation of the storage capacity.
On the other hand, the assessment of the rotational contribution to the partition function requires knowledge of the anisotropy of the adsorption
potential.
For the 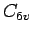 minimum of the H2-benzene PES, the MP2/cc-pVTZ binding energy is -395 cm
minimum of the H2-benzene PES, the MP2/cc-pVTZ binding energy is -395 cm . Binding energies of -261 cm
. Binding energies of -261 cm are found for the corresponding
are found for the corresponding 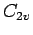 -symmetric structures with H2 perpendicular to any of the benzene
-symmetric structures with H2 perpendicular to any of the benzene 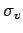 symmetry
planes.
Due to the large rotational level spacing of the H2 molecule (
symmetry
planes.
Due to the large rotational level spacing of the H2 molecule (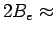 122 cm
122 cm ) and the effects of the nuclear spin statistics, the explicit treatment of the restricted rotation in this potential leads to a small (
) and the effects of the nuclear spin statistics, the explicit treatment of the restricted rotation in this potential leads to a small (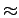 3 %; see section 1.1.4) increase in the adsorption constants, neglected in the calculations.
3 %; see section 1.1.4) increase in the adsorption constants, neglected in the calculations.
Dispersive interactions between the graphene layers were not explicitly considered in these simulations as this approach is equivalent to assume that the layered host structure remains unchanged upon H2 uptake.
Because of the significant free energy cost, associated with the graphene layer separation process (see ref. graphtherm and section 4.1), the ``empty'' layered structure must be stabilised by other means, such as spacers (see ref. Deng2004 and next chapter for examples).
Meaningful calculations of the free energy changes require that
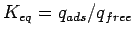 is converged with respect to the volume of the unit
cell.
From test calculations on the single-layer graphene structure, it is found that unit cell
is converged with respect to the volume of the unit
cell.
From test calculations on the single-layer graphene structure, it is found that unit cell 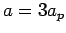 ,
, 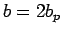 leads to
leads to 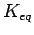 values converged to better than 15 %, therefore all calculations related to graphene sheets use these unit cell dimensions.
Because tunnelling of H2 through the graphene layer is associated with a very high barrier, there is no need to consider unit cells replication in the
values converged to better than 15 %, therefore all calculations related to graphene sheets use these unit cell dimensions.
Because tunnelling of H2 through the graphene layer is associated with a very high barrier, there is no need to consider unit cells replication in the 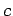 direction.
direction.
Lyuben Zhechkov
2007-09-04
![]() ,
, ![]() ,
, ![]() 1.421 Å) in
1.421 Å) in ![]() and
and ![]() directions.
However, to avoid the attractive artifacts of the
directions.
However, to avoid the attractive artifacts of the ![]() potential close to the nuclei and reduce the requirements for high-frequency basis set components, the simulation cell extent in the
potential close to the nuclei and reduce the requirements for high-frequency basis set components, the simulation cell extent in the ![]() direction
direction![]() for this particular series of structures (see section 1.1.1)
for this particular series of structures (see section 1.1.1)![]() was truncated by
was truncated by ![]() (1.0
(1.0 ![]()
![]()
![]() 2.0 Å) in the vicinity of the graphene sheet(s).
For double-layer structures with interlayer spacing
2.0 Å) in the vicinity of the graphene sheet(s).
For double-layer structures with interlayer spacing ![]() , the unit cell extent in the
, the unit cell extent in the ![]() direction is, therefore,
direction is, therefore,
![]() . Single-layer simulations were
performed by using the same periodic boundary conditions, but the
interlayer spacing
. Single-layer simulations were
performed by using the same periodic boundary conditions, but the
interlayer spacing ![]() was chosen to be large. The unit cell parameters,
together with the plane wave cutoffs, are given in Table 3.1.
was chosen to be large. The unit cell parameters,
together with the plane wave cutoffs, are given in Table 3.1.
![]() minimum of the H2-benzene PES, the MP2/cc-pVTZ binding energy is -395 cm
minimum of the H2-benzene PES, the MP2/cc-pVTZ binding energy is -395 cm![]() . Binding energies of -261 cm
. Binding energies of -261 cm![]() are found for the corresponding
are found for the corresponding ![]() -symmetric structures with H2 perpendicular to any of the benzene
-symmetric structures with H2 perpendicular to any of the benzene ![]() symmetry
planes.
Due to the large rotational level spacing of the H2 molecule (
symmetry
planes.
Due to the large rotational level spacing of the H2 molecule (![]() 122 cm
122 cm![]() ) and the effects of the nuclear spin statistics, the explicit treatment of the restricted rotation in this potential leads to a small (
) and the effects of the nuclear spin statistics, the explicit treatment of the restricted rotation in this potential leads to a small (![]() 3 %; see section 1.1.4) increase in the adsorption constants, neglected in the calculations.
3 %; see section 1.1.4) increase in the adsorption constants, neglected in the calculations.
![]() is converged with respect to the volume of the unit
cell.
From test calculations on the single-layer graphene structure, it is found that unit cell
is converged with respect to the volume of the unit
cell.
From test calculations on the single-layer graphene structure, it is found that unit cell ![]() ,
, ![]() leads to
leads to ![]() values converged to better than 15 %, therefore all calculations related to graphene sheets use these unit cell dimensions.
Because tunnelling of H2 through the graphene layer is associated with a very high barrier, there is no need to consider unit cells replication in the
values converged to better than 15 %, therefore all calculations related to graphene sheets use these unit cell dimensions.
Because tunnelling of H2 through the graphene layer is associated with a very high barrier, there is no need to consider unit cells replication in the ![]() direction.
direction.